关于弹道
相关插件
弹道核心:
◆Drill_CoreOfBallistics 数学模型 - 弹道核心
相关子插件:
◆Drill_CoreOfGaugeMeter 系统 - 参数条核心
◆Drill_CoreOfShatterEffect 系统 - 方块粉碎核心
◆Drill_CoreOfSelectableButton 系统 - 按钮组核心
◆Drill_STG__core STG - 引擎
弹道: 是指能够描述 单个或一群 粒子/碎片/子弹运动的轨迹,是程序经过数学计算后的结果数据集。此定义与实际的弹道学有一些区别。
弹道模式: 指用于描述弹道的各种配置方法。如下图:

由于弹道同时涉及 数学公式和代码定义 ,且许多插件都基于弹道移动,所以此文档需要全文反复学习。(多次简单过目该文档即可)
插件关系
弹道核心属于数学计算,服务于其他各类插件,关系如下:

弹道模式
相关 子插件 会根据自身特殊的情况,
提供部分模式的设置,但不一定会提供所有弹道模式的支持。
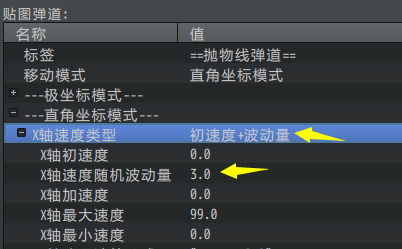
直角坐标模式
直角坐标模式通过 x速度 + y速度 控制轨迹。
时间、速度已知,路程未知。
| X速度(vx):正数向右,负数向左。单位 像素/帧。见 类型 - 速度 。Y速度(vy):正数向下,负数向上。单位 像素/帧。见 类型 - 速度 。(注意,y速度正数向下,是反的。) |
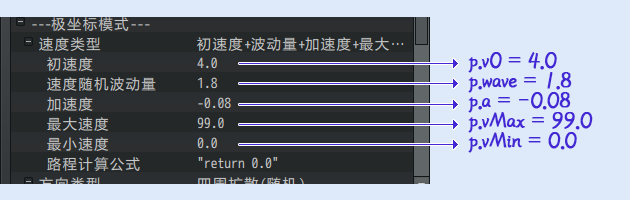
极坐标模式
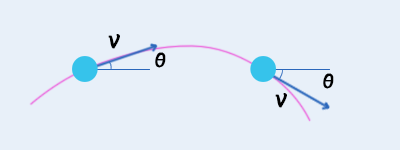
极坐标模式通过 速度+方向 控制轨迹。
时间、速度已知,路程未知。
| 速度(v):正数沿着方向移动,负数反向移动。单位 像素/帧。见 类型 - 速度 。方向(θ):0朝向右,90朝下,-90朝上,顺时针规律。单位 角度。见 类型 - 方向 。(可以写超过360的数。390度与30度的方向一样。) |
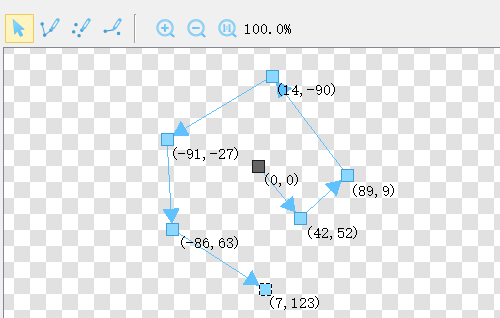
轨道锚点模式
轨道锚点模式中,轨迹是固定的,通过速度,来确定在轨迹中的具体位置。
简单来说,就好比铺火车轨道,无论火车如何加速减速,都一定按照固定轨道到移动,不可能脱轨移动。
设置锚点 = 铺火车轨道
设置速度 = 火车速度变化
| 速度(v):正数沿着轨道移动,不支持负数。单位 像素/帧。见 类型 - 速度 。轨道锚点:绘制固定的锚点列表。单位像素。见 类型 - 轨道锚点 。(只适合单个粒子移动,多个粒子移动效果不明显。) |

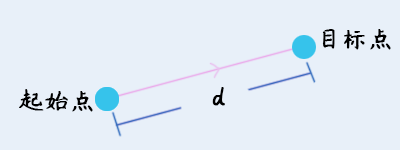
两点式
两点式通过 固定模式+目标点 控制轨迹。
时间、路程已知,速度未知。
起始点: 粒子移动前所在的位置。
目标点: 分为绝对坐标与相对坐标,用于计算当前物体到目标物体的路程。
| 固定模式: 由于时间和路程是固定量,只有速度是可控制变量。根据速度的不同变化方式,可分成多种模式。见 类型 - 两点式 。(只适合 单个对象 移动,多个对象 会重叠。) |
参数类型
类型 - 速度
1)初速度
公式参数名:p.v0 。
速度1,表示 1像素/帧。 速度1.5,表示 1.5像素/帧。
速度可以为负数,表示反方向移动。
只有初速度时,表示匀速运动,可见:公式:只初速度。
2)随机波动量
公式参数名:p.wave 。
在粒子的速度的基础上,添加/减少的随机速度量。
比如,初速度为10,波动量为8,那么速度为:6~14之间。(10-4 ~ 10+4)
初速度+波动量 仍然为匀速运动,可见:公式:初速度+波动量。
3)加速度
公式参数名:p.a 。
粒子在运动过程中,速度逐渐改变的加速度值。
极坐标模式中:无论加速度如何变化,都不会影响运动方向。
直角坐标模式中:如果vy的加速度化和vx的加速度不一样,那么就会间接改变这个粒子的实际方向。比如,vx匀速+vy匀加速 = 抛物线。
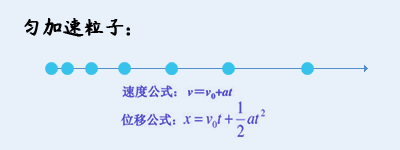
4)速度最大/最小值
公式参数名:p.vMax p.vMin 。
设置限制后,无论速度如何变化,都会保持在最大速度和最小速度之内。
比如,一个不断减速的粒子,如果设置了最小速度0,则会停下来。否则粒子速度将会越来越小,变成负数,朝反方向开始移动。
5)路程计算公式
见后面的章节 路程计算公式 。
类型 - 方向
1)方向单位
主要方向单位为 角度 ,部分设置里面可能会使用弧度,360(角度)= 2π(弧度)。
如果特殊情况要求输入弧度时,可用3.14代替π。
2)四周扩散
四周扩散,即以中心点为基准,方向随机。
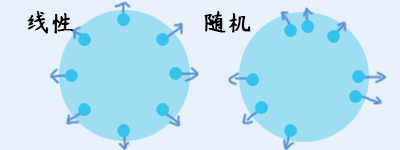
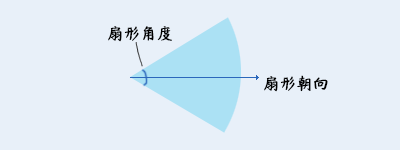
3)扇形范围
图中的朝向的角度为0,90度朝下,-90朝上,顺时针规则。
扇形角度为360时 = 四周扩散
4)方向计算公式
见后面的章节 方向计算公式 。
类型 - 轨道锚点
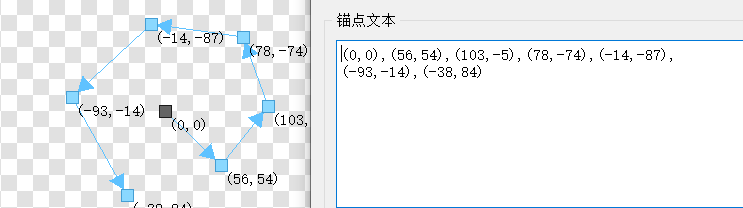
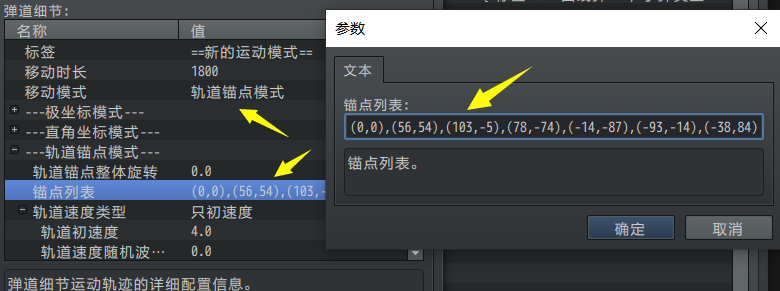
1)锚点列表
这里的轨道,可以通过弹道绘制器绘制出来,从而形成锚点列表。
子弹会根据锚点列表描绘的轨迹,依次进行轨道移动。

2)限时问题
注意,虽然粒子会按照指定的轨道移动,但是粒子 不一定会 走完全部轨道。
粒子的移动时间结束后,粒子会 停在 当前的位置。
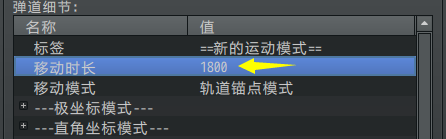
1800帧 = 30秒(可以设置时间长一点,但是不要超过5000,会影响计算速度)
类型 - 两点式
两点式被 窗口、按钮组、图片 等相关插件频繁使用。
其最大的特点就是时间固定,并且最终时间一定会到达终止点。
1) 不移动
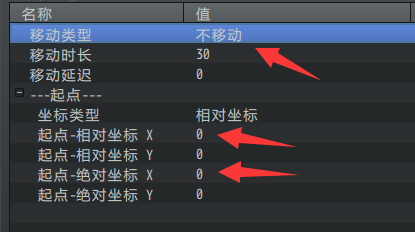
不移动指:指定的对象仍然会保持在起始点,永远 不会 到目标点。
不移动就是字面意思上的真的不移动。
窗口设置不移动时,通常偏移的 坐标 也需要置零。
因为如果没置零,会造成窗口长期停滞在 起始点 ,而不是在原位置。
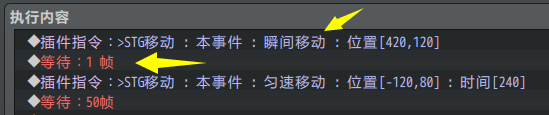
2) 瞬间移动
瞬间移动顾名思义,瞬间移动到目标点。
(设置匀速移动,移动时间为1帧,与瞬间移动的原理是一样的。)
注意,插件指令执行 并不能立刻到达目标点,需要1帧的准备时间。
因此,执行瞬间移动的指令时,需要等待一帧。
3) 匀速移动
匀速移动根据 已知路径 除以 已知时间 得到速度。
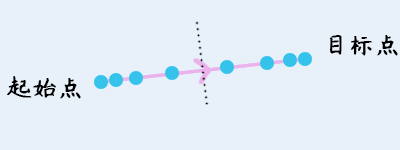
4) 增减速移动
增减速移动中,路程被分为两个部分,前半部分是匀加速,后半部分是匀减速。
5) 弹性移动
弹性移动实际上就是是有初速度的匀减速移动,只是这种移动看起来更加自然而已。
6) 抛物线移动
抛物线移动会额外受到 初速度+方向 的影响,但最终一定会到达目标点。
如果方向与目标点一致,则效果为匀加速运动。
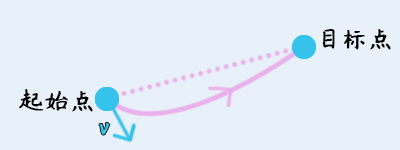
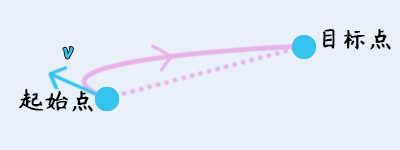
注意,粒子到达终止点后,终止点的速度绝对值一般都会比起始点的速度绝对值大。也就是说,如果持续进行抛物线移动,那么甩动的轨迹会越来越大。
数学公式
公式关系
具体公式脚本,你可以直接用文本打开 插件脚本 进行查看学习哦。
可用变量与常量
变量:是指在游戏中,随时变化的量。
可以简单理解为:插件指令调用,设置的数字,就是变量。
常量:是指在游戏编辑器中,配置的固定的量,在游戏中不会变化。
可以简单理解为:打开插件配置,然后你在配置里面设置了一个固定的值。
速度、加速度等设定,都是通过路程计算公式配置的。
无论是极坐标模式,还是直角坐标模式,路程都决定了粒子最终所在的位置。
直接写数字常量
直接写数字常量:如果你使用的是公式,那么可以直接写数字代替常量,因为常量只是一个可扩展编辑的量,在游戏中不会变化。
举个例子,速度公式如下:
| var result = p.v0 * p.time; //(速度x时间)return result; |
如果你在配置中写了初速度:5.0,
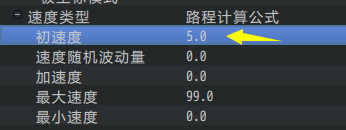
那么与你写的下面的自定义公式是完全一样的:
| var result = 5 * p.time; //(速度x时间)return result; |
注意,p.time不能写成数字,因为在游戏中是实时变化的量。
如果公式中没有变量,那么这个粒子将持续固定在一个具体的位置。
路程计算公式
可用变量与常量
变量:是指在游戏中,随时变化的量。
常量:是指在游戏编辑器中,配置的固定的量,在游戏中不会变化。
| 变量名 | 中文名 | 取值范围 | 描述 |
| p.index | 粒子序号值 | 整数,0 至 p.num-1值 | 粒子定义的Id序号值。 |
| p.time | 时间值 | 整数,0 至 游戏中设定的时间值 | 移动的时间范围值。 |
| p.ran | 随机值 | 小数,0.0 至 1.0 范围随机值 | 插件内部的可控随机值,不建议用Math.random()。 |
| p.num | 粒子数量 | 整数,游戏中设定的粒子数量 | 游戏中设定的粒子数量。 |
| 常量名 | 中文名 | 说明 |
| p.v0 | 初速度 | 无特殊规定。 |
| p.wave | 波动量 | 一般该常量与随机值一起使用。 |
| p.a | 加速度 | 无特殊规定。 |
| p.vMax | 最大速度 | 无特殊规定。 |
| p.vMin | 最小速度 | 无特殊规定。 |
公式关系说明可以看前面章节:公式关系 。
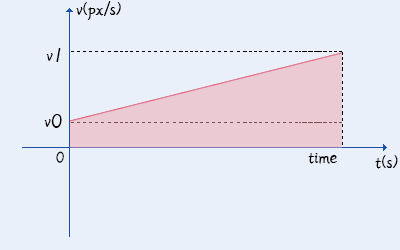
公式:只初速度
众所周知,r = v*t,路程=时间*速度。
匀速运动的情况最简单,长方形面积就是路程。
只初速度的v-t图
公式如下:
用到了 变量 p.time,常量 p.v0 。
| var result = p.v0 * p.time; //(速度x时间)return result; |
公式:初速度+波动量
波动量是指,初速度有一定的随机性,可以在上下进行浮动。
比如 vRan值为 5.0,则浮动范围为 -2.5 ~ 2.5 之间。
简单来说,就是在初速度公式上,额外增加一个波动变化的量。
在出现大量粒子时,通过波动量能够有效让他们散开。
初速度+波动量的v-t图
公式如下:
用到了 变量 p.time/p.ran,常量 p.v0/p.wave 。
| var v_ran = p.wave * (p.ran - 0.5); //(根据波动量,算出波动速度)var result = (p.v0 + v_ran) * p.time; //(随机速度x时间)return result; |
需要注意的是,如果vRan波动量比v0初速度还大,那么就会出现速度为负值的情况。
速度为负,则会朝 相反 的方向移动。
初速度+波动量的v-t图
公式:初速度+波动量+加速度
匀加速运动的公式为:r=vt+½at²,也就是图中的长方形和三角形的和。
v0为初速度,a为加速度,time为时间。
则图中的v1=v0+a*time。
则公式为: v0*time+0.5*a*time*time
初速度+波动量+加速度的v-t图
公式如下:
用到了 变量 p.time/p.ran,常量 p.v0/p.wave/p.a 。
| var v_ran = p.wave * (p.ran - 0.5); //(根据波动量,算出波动速度)var result = (p.v0 + v_ran) * p.time + 0.5 * p.a *p.time*p.time;return result; |
(如果你熟悉js的一些数学函数用法,也可以使用 Math.pow(time,2) 表示时间的平方 )
如果出现 速度v0 为负数情况,公式依然成立。
你将会看到一个粒子逐渐停下,然后朝反方向持续加速的过程。
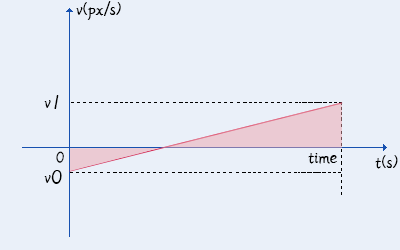
初速度+波动量+加速度的v-t图
公式:初速度+波动量+加速度+最大最小
最大速度和最小速度是一个十分特殊的情况。
它会将速度变化分成多段。
如果速度超出了最大速度,那么就减去vMax多出的面积。
如果速度低于了最小速度,那么就加上vMin多出的面积。
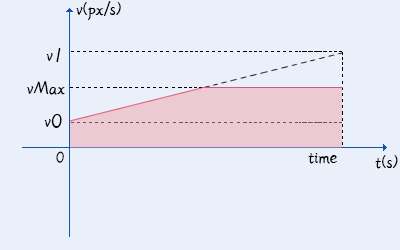
最大速度切割v-t图
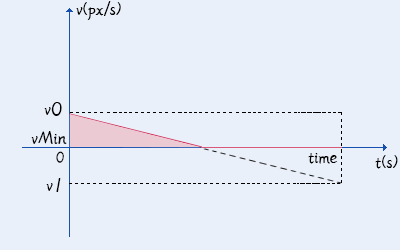
最小速度切割v-t图
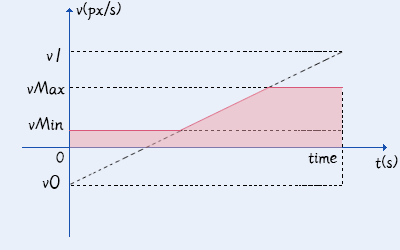
最大最小速度组合切割的v-t图
v0为初速度,a为加速度,time为时间,vMax为最大速度,vMin为最小速度。
公式如下:
用到了 变量 p.time/p.ran,常量 p.v0/p.wave/p.a/p.vMax/p.vMin 。
| var v_ran = p.wave * (p.ran - 0.5); //(根据波动量,算出波动速度)// > 加速度公式var v1 = (p.v0 + v_ran) + p.a * p.time;var d = (p.v0 + v_ran)*p.time + 0.5 * p.a *p.time*p.time;var result = d;// > 分段函数(超过上限/下限,将减去多出的路程值)if( v1 >= p.vMax ){var m_v = v1 - p.vMax;var m_t = (v1 - p.vMax) / p.a;result = d - m_v*m_t + 0.5 * p.a *m_t*m_t;}if( v1 <= p.vMin ){var m_v = v1-p.vMin;var m_t = (v1-p.vMin)/a;result = d - m_v*m_t + 0.5 * p.a *m_t*m_t;}return result; |
自定义公式
当你使用自定义公式时,之前提及的常量(见可用变量与常量)都可以加入设计,
你甚至可以作为其他特殊的参数进行使用。
举个例子,你写了下面的公式:
| var result = p.v0 * p.v0 * p.time * p.id;return result; |
公式中用到了 p.v0常量,那么,
配置类型为:路程计算公式,配置初速度为:5.0

在公式中,将会等价于:
var result = 5.0 * 5.0 * p.time * p.id
你所写自定义公式的 p.v0 真实含义 可能并不表示“初速度”的意思,
但是该参数的确可以作为一个配置值来使用。
注意,设计公式时,常量是最后再考虑加的参数,设计公式时,不要把变量和常量放一起写,会把自己绕晕。
方向计算公式
可用变量与常量
变量:是指在游戏中,随时变化的量。
常量:是指在游戏编辑器中,配置的固定的量,在游戏中不会变化。
| 变量名 | 中文名 | 取值范围 | 描述 |
| p.index | 粒子序号值 | 整数,0 至 p.num-1值 | 粒子定义的Id序号值。 |
| p.time | 时间值 | 整数,0 至 游戏中设定的时间值 | 移动的时间范围值。 |
| p.ran | 随机值 | 小数,0.0 至 1.0 范围随机值 | 插件内部的可控随机值,不建议用Math.random()。 |
| p.num | 粒子数量 | 整数,游戏中设定的粒子数量 | 游戏中设定的粒子数量。 |
| 常量名 | 中文名 | 描述 |
| p.d0 | 固定方向 | 无特殊规定。 |
| p.sFace | 扇形朝向 | 无特殊规定。 |
| p.sDegree | 扇形范围 | 无特殊规定。 |
公式关系说明可以看前面章节:公式关系 。
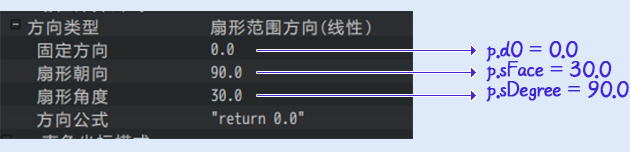
公式:固定方向
指定一个方向,就是一个方向,不会改变。
由于没有改变的成分,所以只用到了常量。
注意,如果你同时发射10个子弹,这10个子弹的 方向 都会重叠在一起,如果其速度配置也没有随机波动量散开,那么将只看到1个子弹。
公式如下:
用到了 变量 无, 常量 p.d0 。
| var result = p.d0; //(固定方向)return result; |
公式:四周扩散
1) 四周扩散(线性)
将一整个圈,按粒子数量平均划分方向值。

公式如下:
用到了 变量 p.index/p.num,常量 p.d0 。
| var result = p.d0 + 360 * p.index / p.num;return result; //(在一个圆圈里,放入固定数量的粒子) |
2) 四周扩散(随机)
将一整个圈,随机划分方向值。
公式如下:
用到了 变量 p.ran,常量 p.d0。
| var result = p.d0 + 360 * p.ran;return result; |
3) 四周扩散(抖动)
抖动功能,是在固定随机方向的基础上,再进行一次随机偏移。
需要注意的是,由于Math.random 的值不可控,这会造成 重复发射/反向弹道 都不能完美复现原有的轨迹,所以尽量少用。
(这个功能其实挺鸡肋,也不知道在什么情况下用的上)
公式如下:
用到了 变量 p.ran,常量 p.d0。
| var result = p.d0 + 360 * p.ran + 30 * Math.random();return result; |
公式:扇形范围方向
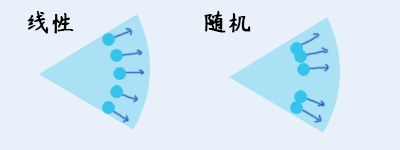
1) 扇形范围方向(线性)
扇形范围,是指以朝向为基准,向两侧撑开的扇形结构。
注意,扇形范围方向,与 p.d0 固定方向的参数没有任何关系。


线性的扇形范围需要区分 只一个粒子 和 有两个或以上 的粒子情况。
单独一个粒子时,发射的朝向就是 扇形朝向 。
公式如下:
用到了 变量 p.index/p.num,常量 p.sFace/p.sDegree 。
| var result = p.sFace;if( p.num > 1 ){result = p.sFace + p.sDegree * p.index / (p.num - 1) - p.sDegree/2;}else{result = p.sFace;}return result; |
2) 扇形范围方向(随机)
随机的扇形范围,就不需要考虑粒子数量问题了。
公式如下:
用到了 变量 p.ran,常量 p.sFace/p.sDegree 。
| var result = p.sFace + p.sDegree * (p.ran - 0.5);//(根据p.sDegree,算出波动范围方向,与朝向相加即可)return result; |
自定义公式
当你使用自定义公式时,之前提及的常量(见可用变量与常量)都可以加入设计,
你甚至可以作为其他特殊的参数进行使用。
举个例子,你写了下面的公式:
| var result = p.d0 * p.d0 * p.time * p.id;return result; |
公式中用到了 p.d0常量,那么,
配置类型为:方向计算公式,配置固定方向为:0.8
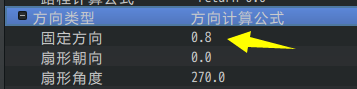
在公式中,将会等价于:
var result = 0.8 * 0.8 * p.time * p.id
你所写自定义公式的 p.d0 真实含义 可能并不表示“固定方向”的意思,
但是该参数的确可以作为一个配置值来使用。
注意,设计公式时,常量是最后再考虑加的参数,设计公式时,不要把变量和常量放一起写,会把自己绕晕。
随机因子
| 随机因子并不是开放的配置项,主要影响与参数”p.ran”的随机值。这里主要为了方便脚本开发,介绍一下的随机因子的作用原理。 |
随机因子与随机种子
随机种子: 是指c++语言中的函数,用法为”rand(种子值)”。
随机因子: 是指drill插件中定义的 与随机种子 类似的结构。
随机因子和随机种子本质上意思一样,只是叫法不一样。
固定了随机种子,能表现出一模一样的"随机"效果。
下图为 多层行走图粒子 插件的效果:

随机迭代次数
随机迭代次数: 指使用同一个 随机因子 的弹道,来生成多条不同弹道的迭代次数。
当一个粒子走完了一条弹道后,它要换一条新的弹道来走。
旧弹道和新弹道基于同一个 随机因子。
通过迭代次数,能实现只用一个随机数,来完全控制一群粒子的移动轨迹。
组合公式效果
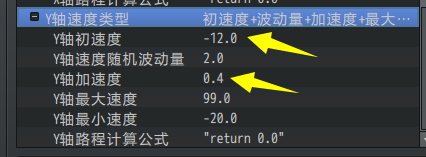
抛物线运动
抛物线是最常用的效果了。
运动轨迹分为x轴和y轴两个方向。(极坐标也可以表示,但是公式比较复杂。)
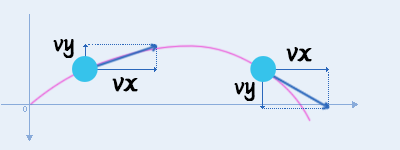
原理不难理解,举个例子:** 平抛运动**(高一物理)
下图中,一个球向一个方向匀速抛出,但是球本身受到 重力加速度 的影响,可以形成一个弧线轨迹。
也就是说,x轴匀速,y轴加速运动,就可以形成抛物线。
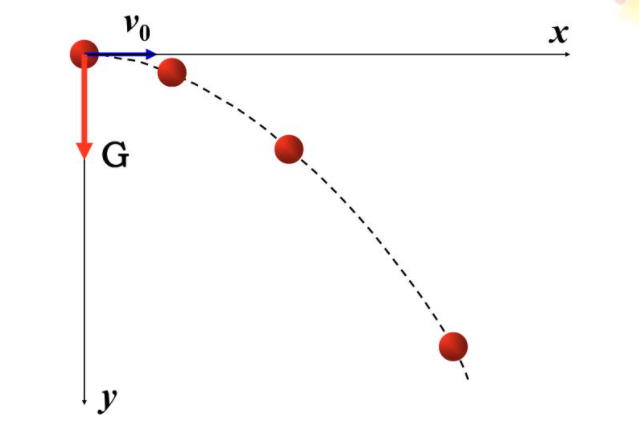
由于平抛运动的y轴初速度是0,所以是一个一直向下的抛物线。
如果y轴初速度是负数,那么可以形成先向上,再向下的抛物线轨迹。
比如 子插件 地图UI-漂浮参数数字 配置抛物线弹道后,实现的喷泉抛物线。